Set Theory

A set is a collection of distinct objects. A set simply specifies the contents, the order is not important. $\{1,2,3\}$ is the same as $\{3,1,2\}$.

A set doesn't have to contain numbers, you could, for example, have a set of the base colors $\{red, green, blue\}$ you are not limited in this regard, Important is that they are distinct.

If we have the set $A=\{a,b,c\}$. To indicate that an object is an element/member of the set $A$ you write $a \in A$. To indicate that an object is not an element of a set you write $z \notin A$.

Sets are characterized by their elements. Thus, two sets are only equal if they have the same elements. If $B=\{a,b,c\}$ then $A=B$. However $C=\{a,b,c,d\}$ and therefore $A \neq C$.

There is only one set with no elements at all, the empty set, and is represented by the symbol $\emptyset$. You may also see $\{\}$ being used.

Notations

There are multiple ways to define a set.

Roster Notation

The roster or also called enumeration notation defines a set by listing its elements between curly brackets separated by commas.

For example $A=\{1,2,3\}$

Set-Builder Notation

This is probably the hardest notation to understand. The set-builder notation specifies a set as a selection from a larger set, determined by a condition on those elements.

For example $F = \{ a \mid a \text{ is an integer, and } 0 \leq a \leq 5\}=\{0,1,2,3,4,5\}$ The vertical bar, "|" means "such that". So the description can be read as "F is the set of all numbers n such that n is an integer in the range from 0 to 5 inclusive.

Semantic Definition

Sets can also be described using words and rules.

Let $A$ be the first 3 positive integers that are odd. So $A=\{1,3,5\}$ Let $B$ be the set of colors of the French flag. So $B=\{red,green,blue\}$

Sets of Numbers

A good visualization for the set of numbers.

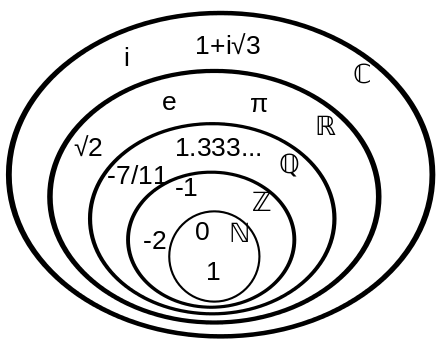
Natural Numbers

$\Bbb{N} =\{0, 1,2,3,...\}$ some authors do not include 0 in the set of natural numbers. These authors then use the following notation to include 0 $\Bbb{N}_0 =\{0,1,2,3,..\}$. I prefer to include 0 and in the special cases where I do not want it to be included I can use set subtraction/difference $\Bbb{N} \setminus \{0\} = \{1,2,3,...\}$.

Integers

$\Bbb{Z} =\{...,-2,-1,0,1,2,...\}$

Multiple variations and combinations are also possible:

• $\Bbb{Z}^+ =\{1,2,3,...\}=\Bbb{N}\setminus \{0\}$
• $\Bbb{Z}^- =\{...,-3,-2,-1\}$
• $\Bbb{Z}_0^+ =\{0,1,2,3,...\}=\Bbb{N}$ combinations are also possible.

Rational Numbers

todo

including proof of why sqrt(2) is not a rational number but irrational

Real Numbers

todo

Complex Numbers

The set of complex numbers is denoted with $\Bbb{C}$. You can see what complex numbers are and how they are used on this page or also just look at a cheat sheet to refresh your knowledge (will however be in german).

Sub and Superset

$A$ is a subset of a set $B$ if all elements of $A$ are also elements of $B$. $B$ is then a so called superset of $A$.

In the above case It is possible for $A$ and $B$ to be equal. if they are unequal but a subset, then $A$ is a so called proper subset of $B$.

The notations for the relations mentioned above can be very different see here. I will however be using the following notations:

• For $A$ is a subset of $B$: $A \subseteq B$
• For $B$ is a superset of $A$: $B \supseteq A$
• For $A$ is a proper subset of $B$: $A \subset B$
• For $B$ is a proper superset of $A$: $B \supset A$

It's a big help if you imagine sets as circles by doing so you can easily visualize things like the following:

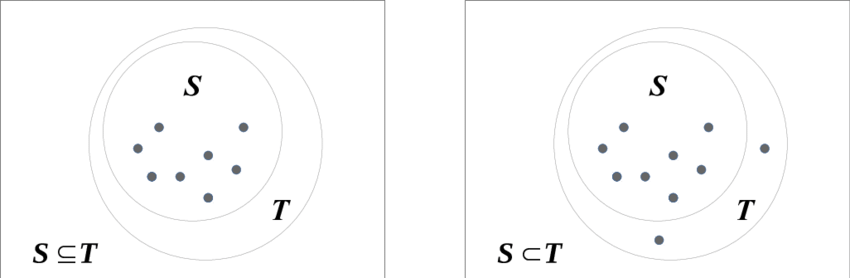
Notice that $\emptyset \subseteq A$, for any set $A$.

Ordered Pair

An ordered pair $(a,b)$ is a pair of objects. The order in which the objects appear in the pair is significant: the ordered pair $(a,b)$ is different from the ordered pair $(b,a)$ unless$a=b$. In contrast, the unordered pair $\{a,b\}$ equals the unordered pair $\{b,a\}$.

Basic Set Operations

There are several fundamental operations for constructing new sets from given sets.

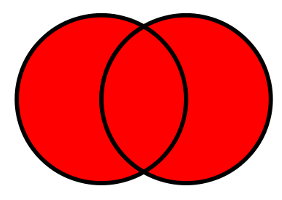
Union

Two sets can be joined together, this results in the so called union of $A$ and $B$. This is written as $A \cup B$. The union is the set containing all elements that are in $A$ or $B$ or both.

example

$$\begin{align*} \{1,2\} \cup \{1,2\} &= \{1,2\} \\ \{1,2\} \cup \{2,3\} &= \{1,2,3\} \\ \{1,2,3\} \cup \{3,4,5\} &= \{1,2,3,4,5\} \end{align*}$$

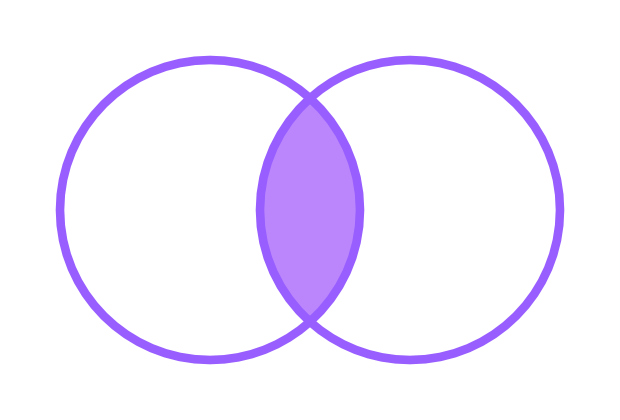
Intersection

A new set can also be constructed by determining which elements two sets have "in common", this results in the so called intersection of $A$ and $B$. This is written as $A \cap B$. The intersection is the set of all things that are elements of both $A$ and $B$. If $A \cap B = \emptyset$, then $A$ and $B$ are called disjoint.

example

$$\begin{align*} \{1,2\} \cap \{1,2\} &= \{1,2\} \\ \{1,2\} \cap \{2,3\} &= \{2\} \\ \{1,2\} \cap \{3,4\} &= \emptyset \end{align*}$$

Complements

The so called absolute complement of $A$ (or simply the complement of $A$) is the set of elements not in $A$. In other words, let $U$ be a set that contains all the elements under study. If there is no need to mention $U$, either because it has been previously specified, or it is obvious (for example all positive numbers). Then the absolute complement of $A$ is the difference (Or relative complement) of $A$ in $U$. This can be written as $A^c = U \setminus A$.

example

$$\begin{align*} \{1,2\} \cap \{1,2\} &= \{1,2\} \\ \{1,2\} \cap \{2,3\} &= \{2\} \\ \{1,2\} \cap \{3,4\} &= \emptyset \end{align*}$$

Difference

If $B$ and $A$ are sets, then the relative complement (or short difference) of $B$ and $A$, is the set of elements in $B$ without the elements of $A$. This can be written as $B \setminus A$.

example

$$\begin{align*} \{1,2,3\} \setminus \{2,3,4\} &= \{1\} \\ \{2,3,4\} \setminus \{1,2,3\} &= \{4\} \\ \{1,2,3\} \setminus \{1,2,3,4\} &= \emptyset \end{align*}$$

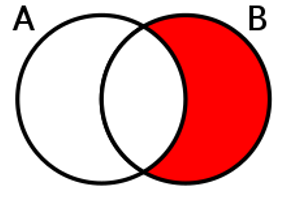
Symmetric Difference

The symmetric difference of two sets (also known as the disjunctive union), is the set of elements which are in either of the sets, but not in both sets (their intersection). This can be written as $A \ominus B$ or $A \triangle B$ which can however cause confussion with other subjects. The symmetric difference can be defined as $A \ominus B=(A \cup B)\setminus (A \cap B)$ or as $(A \setminus B)\cup(B \setminus A)$.

example

$\{7,8,9,10\} \ominus \{9,10,11,12\} = \{7,8, 11,12\}$

Cartesian Product

The Cartesian product of two sets $A$ and $B$, denoted by $A \times B$, is the set of all ordered pairs $(a,b)$ where $a$ is an element of $A$ and $b$ is an element of $B$. So in short a set of all of the possible combinations.

example

$\{1,2\} \times \{3,4\} = \{(1, 3), (1, 4), (2, 3), (2, 4)\}$

Cardinality

The cardinality of a set $A$ is the number of elements/members of $A$. This can be written as $|A|$.

If $A=\{1,2,3\}$ then $|A|=3$

Repeated elementes in roster notation are not counted, so $B=\{blue, white, red, blue, white\}$ then $|B|=3$

Power Set

The power set or also called super set of a set $A$ is the set containing all subsets of $A$. The empty set and $A$ itself are also elements of the power set of $A$, because these are also both subsets of $A$.

The power set of the set $A$ is commonly written as $P(A)$ or $2^{A}$

example

Given $A={x,y,z}$:

$S^A=P(A)=\{\emptyset,\{x\},\{y\},\{z\},\{x,y\},\{x,z\},\{y,z\},\{x,y,z\}\}$

Cardinality of a Power Set

The amount of elements in a power set is pretty easy to calculate. If $|A|=3$ as in the example above then $|P(A)|=2^3=8$ which can simplified to $|P(A)|=2^{|A|}$, this is why I prefer to use the $P(A)$ notation as the other notation can quickly cause confusion.

Partitions

A partition of a set $A$ is a set of non-empty subsets of $A$ such that every element $a \in A$ is in exactly one of these subsets.

The set $P$ is only a partition of $A$ if and only if all of the following conditions hold:

• P does not contain the empty set, so $\emptyset \notin P$.
• The union of all the sets in $P$ is equal to $A$.
• The intersection of any two distinct sets in $P$ is the empty set, $\emptyset$

example

The set $\{1,2,3\}$ has 5 possible partitions:

• $\{\{1\},\{2\},\{3\}\}$
• $\{\{1,2\},\{3\}\}$
• $\{\{1,3\},\{2\}\}$
• $\{\{1\},\{2,3\}\}$
• $\{\{1,2,3\}\}$

The following are not partitions of {1,2,3}:

• $\{\emptyset,\{1,3\},\{2\}\}$ is not a partition because one of its elements is the empty set.
• $\{\{1,2\},\{2,3\}\}$ is not a partition because the element 2 is contained in more than one block.
• $\{\{1\},\{2\}\}$ is not a partition of $\{1,2,3\}$ because none of its blocks contains the element 3.

De Morgan's Laws

todo